SHKOLO.RUПараллелограмм и трапеция
Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.
Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.
Свойства параллелограмма
1. Противолежащие стороны равны.
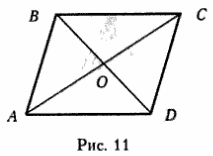
На рис. 11 AB = CD; BC = AD.
2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A = ∠C; ∠B = ∠D.
3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.
На рис. 11 отрезки AO = OC; BO = OD.
Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.
Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Виды трапеций
1. Трапеция, у которой боковые стороны не равны,
называется разносторонней (рис. 12).
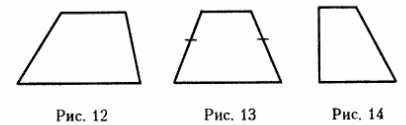
2. Трапеция, у которой боковые стороны равны, называется равнобокой (рис. 13).
3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной (рис. 14).
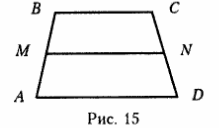
Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN). Средняя линия трапеции параллельна основаниям и равна их полусумме.
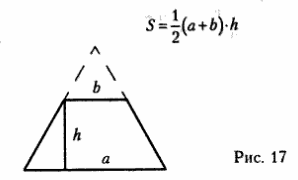
Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).
Площадь параллелограмма и трапеции
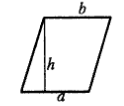
Правило. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Правило. Площадь трапеции равна произведению полусуммы ее оснований на высоту (рис. 17).
У прямоугольной трапеции (рис. 14) высотой служит боковая сторона, перпендикулярная основаниям. Вместо полусуммы оснований трапеции 
можно взять длину средней линии трапеции (на рис. 15 отрезок MN).