Равенство геометрических фигур и площадь фигуры

Для обозначения равенства фигур используется знак равенства в кратком наименовании фигур.

Пример. Два треугольника равны, но один по отношению к другому смещен но плоскости листа и повернут на 180°. ΔABC = ΔA₁B₁C₁.

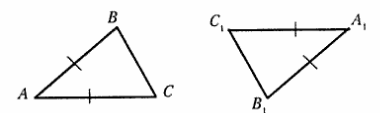
Два треугольника равны, если у них соответствующие стороны и соответствующие углы равны.

Тогда ΔABC = ΔA₁B₁C₁ если:

1) AB = A₁B₁ BC = B₁C₁ AC = A₁C₁
2)∠A = ∠A₁ ∠B = ∠B₁ ∠C = ∠C₁

Равные фигуры имеют равные площади.

Существуют формулы площади для всех простейших многоугольников и круга. Для составных фигур площадь определяется как сумма площадей простых фигур. Так, шестиугольник можно разбить па 2 треугольника и четырехугольник, определить площади каждого из них, а потом сложить.

Единицами площади служат единицы измерения длинны (мм, дм, см, м, км) в квадрате (перемноженные дважды: мм², см², дм², м², км²) или специальные единицы площади (ар, или «сотка»; гектар).

Единицы площади — величины взаимосвязанные:
1 см² = 100 мм²
1 дм² = 100 см²
1 м² = 100 дм² = 10 000 см²

1 км² = 1 000 000 м²
1а = 100 м²
1 га = 100 а = 10 000 м².

Формулы для вычисления площади простых геометрических фигур

S = a ²

Площадь квадрата, где а — сторона квадрата.

S = a * b

Площадь прямоугольника, где а — длина; Ь — ширина прямоугольника.

S = ½ * a * h

Площадь треугольника, где а — сторона треугольника; Н — высота треугольника, проведенная к этой стороне.

Если фигура сложной конфигурации состоит из нескольких простых фигур, то необходимо посчитать по формулам площади простых фигур, а потом эти площади сложить.