Прямая призма
Многогранником называется такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Прямая призма относится к простейшим многогранникам. Каждая грань (многоугольник, ограничивающий многогранник) многогранника расположена в своей плоскости. Пересечение граней многогранника проходит по линии его ребер.
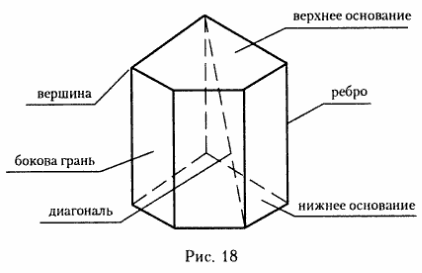
На рис. 18 — пятигранная прямоугольная призма (в основании призмы лежит пятиугольник). У нее 10 вершин; 5 боковых граней; 2 основания (верхнее и нижнее). Для прямоугольной призмы высотой служит любое ребро, расположенное перпендикулярно основанию.
Боковые грани прямоугольной призмы — прямоугольники. Сумма площадей этих прямоугольников составляет площадь боковой поверхности призмы.
Площадь поверхности призмы состоит из суммы площадей двух (одинаковых) оснований и площади боковой поверхности.
Определение. Призма — это многогранник, у которого две грани, называемые основаниями, — равные многоугольники, а все остальные — боковые грани, состоящие из параллелограммов, плоскости которых параллельны одной прямой, называемой ребром многогранника.
Высота призмы — это расстояние между ее основаниями. Для прямой призмы, у которой все ребра перпендикулярны основаниям, — это любое из ребер.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы.
Разверткой призмы называется перенос без искажения размеров всех ее граней в одну плоскость. Развертка призмы, изображенной на рис. 18, приведена на рис. 19.
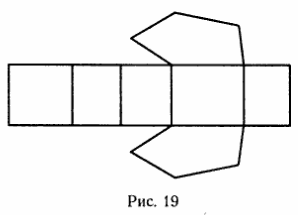
На рис. 19 прямоугольник, разделенный ребрами на 5 меньших прямоугольников, составляет развертку боковой поверхности, а сверху и снизу от нее расположены многоугольники верхнего и нижнего оснований. Площадь всей этой фигуры и составит полную площадь поверхности призмы.
Правило. Площадь боковой поверхности призмы равна произведению периметра основания и высоты.
Sбок = p * h
где:
Sбок — площадь боковой поверхности
p — периметр основания призмы (многоугольника, лежащего в основании);
h — высота призмы (для прямоугольной — это длина бокового ребра призмы).
Правило. Объем прямой призмы равен произведению площади основания н длины бокового ребра.
V = Sбок * l
где:
V — объем призмы;
Sбок — площадь основания призмы (многоугольника, лежащего в основании призмы);
l — длина бокового ребра призмы.
 SHKOLO.RU
SHKOLO.RU