Уравнения

Уравнение — это равенство, содержащее букву, знамение которой нужно найти. Решение уравнения — это тот набор значений букв, при котором уравнение превращается в верное равенство:

Напомним, что для решения уравнении надо слагаемые с неизвестным перенести в одну часть равенства, а числовые слагаемые в другую, привести подобные и получить такое равенство:

ах = Ь

Из последнего равенства определим неизвестное по правилу: «один из множителей равен частному, деленному на второй множитель».

x = b : a

Так как рациональные числа а и Ь могут иметь одинаковые и разные знаки, то знак неизвестного определяется по правилам деления рациональных чисел.

Порядок решения линейных уравнений

1. Линейное уравнение необходимо упростить, раскрыв скобки и выполнив действия второй ступени (умножение и деление).

2. Перенести неизвестные в одну сторону от знака равенства, а числа — в другую сторону от знака равенства, получив тождественное заданному равенство,

3. Привести подобные слева и справа от знака равенства, получив равенство вида ax = b.

4. Вычислить корень уравнения (найти неизвестное х из равенства x = b : a),

5. Выполнить проверку, подставив неизвестное в заданное уравнение.

Если получим тождество в числовом равенстве, то уравнение решено верно.

Особые случаи решения уравнений

1. Если уравнение задано произведением, равным 0, то для его решения используем свойство умножения: «произведение равно нулю, если один из сомножителей или оба сомножителя равны нулю».

   Примеры.

   1. 27 (x — 3) = 0
      27 не равно 0, значит x — 3 = 0

      x = 3

   2. (x — 3)(x + 2) = 0

      х — 3 = 0 или x + 2 = 0
      х = 3 или x = -2

      У второго примера два решения уравнения, так как
      это уравнение второй степени:

      (x — 3)(х + 2) = x² + 2x — 3x — 6 = х² — х — 6

2. Если коэффициенты уравнения являются обыкновенными дробями, то прежде всего надо избавиться от знаменателей. Для этого:

   • — найти общий знаменатель;

   • — определить дополнительные множители для каждого члена уравнения;

   • — умножить числители дробей и целые числа на дополнительные множители и записать все члены уравнения без знаменателей (общий знаменатель можно отбросить);

   • — упростить уравнение;

   • — перенести слагаемые с неизвестными в одну часть уравнения, а числовые слагаемые — в другую от знака равенства, получив равносильное равенство;

   • — привести подобные члены;

   • — вычислить неизвестное.

   • 

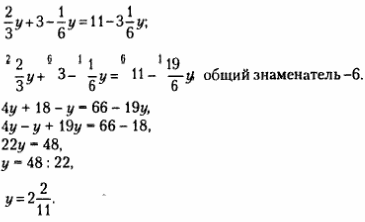
Основные свойства уравнений

1. В любой части уравнения можно приводить подобные слагаемые или раскрывать скобку.

2. Любой член уравнения можно переносить из одной части уравнения в другую, изменив его знак на противоположный.

3. Обе части уравнения можно умножать (делить) на одно и то же число, кроме 0.

В примере выше для решения уравнения были использованы все его свойства.