Цилиндр, конус, шар
Цилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения.
Объемные фигуры вращения (еще говорят — «тела», подразумевая объемность фигуры), как правило, образованы вращением плоской фигуры вокруг какой-то линии (прямой).
Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси.
Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует.
В курсе математики для б класса рассматриваются только прямые цилиндры и конусы
.
Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.
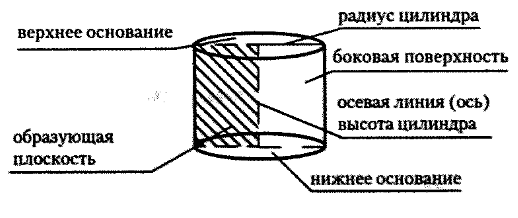
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
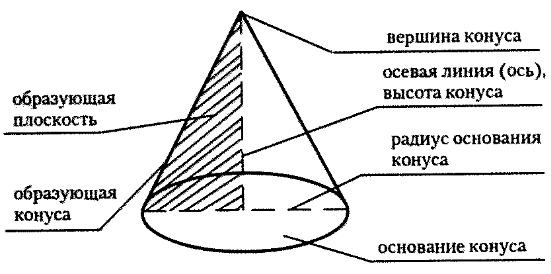
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.
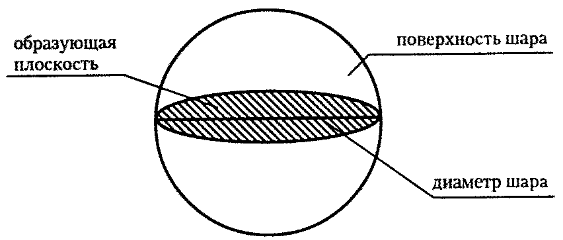
Развертки цилиндра и конуса
Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры.
Развертка цилиндра приведена схематически.
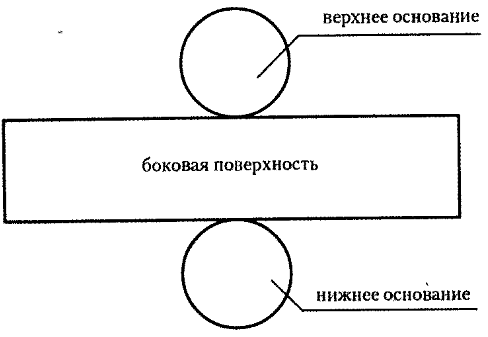
Развертка конуса приведена схематически.
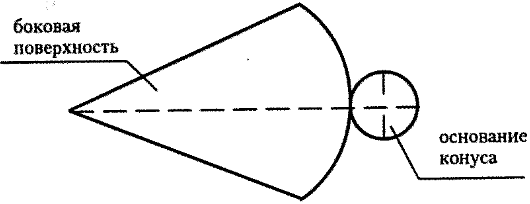
Площади боковой поверхности цилиндра и конуса
Правило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра.
![]()
где C — длина окружности, H — высота цилиндра, R — радиус окружности основания.
Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.
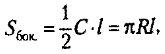
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Площадь поверхности шара
Правило. Площадь поверхности шара равна учетверенной площади большого круга шара.
![]()
где R — радиус шара.
Объемы цилиндра, конуса и шара
Правило. Объем цилиндра равен произведению площади основания н высоты.
![]()
где R — радиус основания, H — высота цилиндра.
Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса.
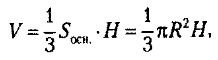
где R — радиус основания, H — высота конуса.
Правило. Объем шара равен четырем третям
произведения числа Пи на куб радиуса.
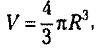
где R — радиус шара.
 SHKOLO.RU
SHKOLO.RU