SHKOLO.RUОсновное свойство дроби
Чтобы сравнить, сложить или вычесть обыкновенные дроби с разными знаменателями, их нужно вначале привести к одинаковому (одному) знаменателю.
Для этого число, от которого взята часть долями (количество долей числа определяет знаменатель), разбивается на большее число долей так, чтобы все знаменатели дробей были кратны между собой.
Например, нужно сравнить, сложить или вычесть дроби 
и 
. Рассмотрим на рисунке дробление на доли (1 разделили на 4 части и 1 разделили на 2 части), за целое принимается 1.
Разделив на 2 доли, получаем наглядное сравнение.
Значит, 
, так как в доли содержится 2 доли по Запишем: 
. По правилам арифметики: 
Выделим простые множители в числителе и знаменателе:
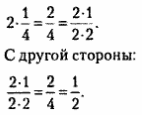
Приведенные рисунки позволяют вывести правило, называемое основным свойством дроби.
Правило. Числитель и знаменатель дроби можно умножать или делить на одно и то же натуральное число, от чего величина дроби не изменяется.
Если числитель новой дроби представить произведением (или частным) первой дроби и любого натурального числа, а знаменатель новой дроби — произведением (или частным) знаменателя первой дроби и того же числа, то новая дробь сохраняет при вычислении произведений (или частных) значение (величину) исходной дроби, поэтому между заданной и полученной дробью можно ставить знак равенства.
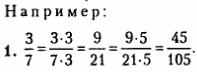
Можно записать основное свойство дроби при умножении числителя и знаменателя дроби на число: 
Можно записать основное свойство дроби при делении числителя и знаменателя дроби на число: 