Запись и чтение десятичных дробей

Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.

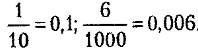
Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.

Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.

Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».

Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.

К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.

Чтение целой части десятичной дроби такое же, как и натуральных чисел.

После целой части десятичной дроби произносится слово «целых».

Десятичные знаки — это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.

• 1-й разряд после занятой — разряд десятых
• 2-й разряд после запятой — разряд сотых
• 3-й разряд после запятой — разряд тысячных
• 4-й разряд после запятой — разряд десятитысячных
• 5-й разряд после запятой — разряд стотысячных
• 6-й разряд после запятой — разряд миллионных
• 7-й разряд после запятой — разряд десятимиллионных
• 8-й разряд после запятой — разряд стомиллионных

В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.

Перевод десятичной дроби в смешанную дробь состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой — числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.

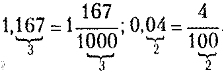
Перевод обыкновенной дроби в десятичную дробь — это вычисление частного отделения числителя дроби на знаменатель по правилам действий с десятичными дробями:

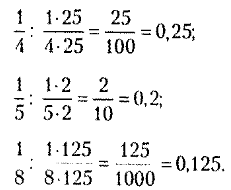
Но не все обыкновенные дроби можно перевести в десятичную дробь. Например:  — нет такого множителя, который с множителем 3 даст в произведении разрядную единицу.