Сложение и вычитание дробей с одинаковыми знаменателями
Следующие правила применяются для правильных и неправильных дробей (смешанную дробь всегда можно перевести в неправильную дробь) с одинаковыми знаменателями.
Правило. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители и оставить тот же знаменатель.
Например: 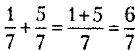
Правило. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби и оставить тот же знаменатель.
Например: 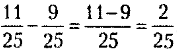
Следующие правила применяются для смешанных дробей с одинаковыми знаменателями.
Правило. Чтобы сложить смешанные дроби, необходимо отдельно сложить их целые и дробные части и записать сумму целых частей и сумму дробных частей смешанной дробью.
Если суммарная дробная часть окажется неправильной дробью, то те следует перевести в смешанную дробь, а выделенную из неправильной дроби целую часть добавить к сумме целых частей. Окончательную сумму целой и дробной частей записать смешанной дробью.
Например, сложить дроби:
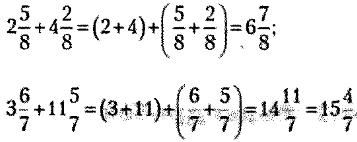
Правило, Чтобы вычесть смешанные дроби, необходимо отдельно вычесть их целые и отдельно их дробные части и записать сумму полученных разностей смешанной дробью.
Если дробная часть уменьшаемого меньше дробной части вычитаемого, то от целой части уменьшаемого «одалживаем» 1, которую представляем как дробь с тем же знаменателем, что и у дробной части смешанных дробей, и с равным этому знаменателю числителем. Одолженную 1, выраженную неправильной дробью с одинаковыми числителем и знаменателем, суммируем с дробной частью уменьшаемого. После этого производим вычисления согласно правилу вычитания смешанных дробей.
Например, вычесть дроби:
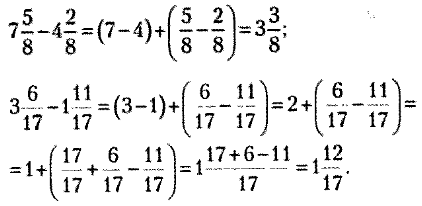
 SHKOLO.RU
SHKOLO.RU