SHKOLO.RUДробные числа
Определение. Обыкновенная дробь — это частное двух чисел, записанное определенным образом. Частное записывается как делимое (верхняя часть дроби) и делитель (нижняя часть дроби), но вместо знака деления между ними стоит горизонтальная черта, которая называется дробной чертой. Делимое называется числителем дроби, а делитель — знаменателем дроби.
Всякая дробь — это часть целого. Чаще всего за целое принимается 1 (единица). Число, записанное в знаменателе, показывает, на сколько более мелких частей делится целое (единица), а число, записанное в числителе, показывает сколько этих более мелких частей объединяются вместе. Это объединение не всех мелких частей единицы соответствует той дроби, ориентируясь на которую, мы делили единицу на более мелкие части и объединяли некоторые из них.
Например: дана дробь — 
.
За единицу принимаем прямоугольник определенной длины (если у дроби нет размерности, то можно делать любые предположения по поводу физического вида целой единицы,
Знаменатель дроби 3. следовательно, наш прямоугольник надо разделить на 3 равные части:
Числитель дроби 2, поэтому из разделенного на 3 части прямоугольника, мы берем только 2 части.
Наша дробь на схеме внизу по сравнению с целым числом (1) оказалась меньше целого.
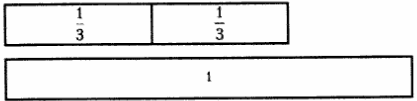
Значит, дробь — это прямоугольник, который меньше целого прямоугольника на 
.
обе части.
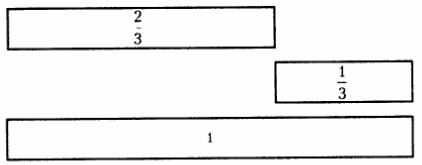
и .На приведенном примере рассмотрим арифметические действии с дробями. Нарисовав отдельно и поместив их рядом ( смотри предыдущий рисунок ), мы произвели вычитание: от целого 1 (уменьшаемого) мы отрезали часть в , следовательно, — это вычитаемое, и получили разность — .
Для того что бы произвести сложение, надо поместить в одном прямоугольнике, принятом за 1 (сумма), наши прямоугольники в и следовательно, оба прямоугольника — это слагаемые.