Прямая и обратная пропорциональность
Две взаимно зависимые величины называются пропорциональными, если отношение их величин остается неизменным. С увеличением (уменьшением) одной величины в несколько раз другая величина увеличивается (уменьшается) во столько же раз.
Определение. Частное величин, составляющих пропорцию, называется коэффициентом пропорциональности. Коэффициент пропорциональности обозначается маленькой латинской буквой k.
- Например:
- 1 : 10 = 0,5 : 5
- 10 : 100 = 5 : 50
- 0,1 : 1 = 0,05 : 0,5
- Коэффициент пропорциональности во всех пропорциях k = 0,1.
Правило. Если две величины связаны между собой так, что увеличение (уменьшение) одной пропорционально (во столько же раз) увеличивает (уменьшает) и другую величину, то такие величины прямо пропорциональны.
Схематически прямую пропорциональность можно записать гак: «больше — больше» или «меньше — меньше». Примерами прямой пропорциональности служит зависимость скорости от пройденного пути, стоимости от веса товара.
Схематически обратную пропорциональность можно записать так: «больше — меньше» или «меньше — больше». Пример обратной пропорциональности: грузоподъемность одной машины и количество машин при перевозке одинакового объема груза.
В краткой схеме условия задачи стрелки прямой и обратной пропорциональности расставляются по-разному.
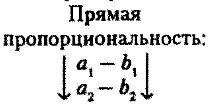
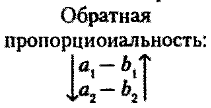
 SHKOLO.RU
SHKOLO.RU
Спасибо вам большое!Очень помогло в домашнем задании))
Теперь я хорошо знаю,что такое обратные и прямые пропорции))