Пропорция
Если у двух отношений одинаковое частное, то их можно соединить знаком равенства, тогда это равенство будет уже пропорцией.
Определение, Равенство двух отношений называется пропорцией.
Пропорции можно записывать в виде частного двух натуральных чисел, обыкновенными дробями, численно и буквенно. Например:
2 : 3 = 8 : 12;
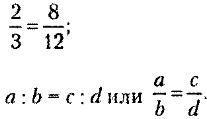
Буквенная запись пропорции a : b = c : d — это общий
вид пропорции, где:
a и d — это крайние члены пропорции;
b и c — это средние члены пропорции.
Основное свойство пропорции: a * d = b * c
Правило . Произведение средних членов истинной пропорции равно произведению ее крайних членов.
Правило. Средние и крайние члены пропорции можно менять местами, от этого пропорция не изменится.
Например, для истинной пропорции a : b = c : d верно: a * d = b * c
Истинными будут и пропорции a : b = b : d, d : b = c : a, d : c = b : a.
В пропорции один из ее членов можно заменить буквой (обозначить буквой неизвестный член пропорции).
Например: 2 : 3 = x : 12 или x : 3 = 8 : 12.
В первом примере неизвестен средний член пропорции, а во втором — ее крайний член.
Пропорция с одним неизвестным часто встречается в решении задач (значение неизвестного — это ответ на вопрос задачи). Вычислить любой член пропорции можно по следующем правилу.
Правило . Неизвестный крайний член пропорции равен частному произведения средних членов пропорции и известного крайнего члена.
Неизвестный средний член пропорции равен частному произведения крайних членов пропорции и известного среднего члена.
Определение неизвестного члена пропорции ![]() :
:
x : b = c : d, x = (b * c) : d
a : b = c : x, x = (b * c) : a
a : x = c : d, x = (a * d) : c
a : b = x : d, x = (a * d) : b
 SHKOLO.RU
SHKOLO.RU