Наименьшее общее кратное
Определение. Наименьшее общее кратное (НОК) двух натуральных чисел — это наименьшее натуральное число, которое делится на эти числа без остатка.
НОК всегда натуральное число, которое должно быть больше самого большого из чисел, для которых оно определяется.
- Правило. Чтобы найти НОК ряда чисел, нужно:
- — разложить числа на простые множители;
- — перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз;
- — полученное произведение простых множителей будет НОК заданных чисел.
Любые два и более натуральных чисел имеют свое НОК. Если числа не кратны друг другу или не имеют одинаковых множителей в разложении, то их НОК равно произведению этих чисел.

Простые множители числа 28 (2, 2, 7) дополнили множителем 3 (числа 21), полученное произведение (84)
будет наименьшим числом, которое делится на 21 и 28 .
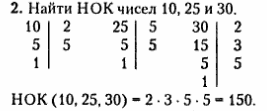
Простые множители наибольшего числа 30 дополнили множителем 5 числа 25, полученное произведение 150 больше самого большого числа 30 и делится на все заданные числа без остатка. Это наименьшее произведение из возможных (150, 250, 300...), которому кратны все заданные числа.

Числа 2,3,11,37 — простые, поэтому их НОК равно произведению заданных чисел.
Правило. Чтобы вычислить НОК простых чисел, нужно все эти числа перемножить между собой.
 SHKOLO.RU
SHKOLO.RU