Наибольший общий делитель
Определение. Наибольший общий делитель (НОД) нескольких чисел — это наибольшее натуральное число, на которое делится каждое из данных чисел. НОД нескольких чисел равен произведению всех общих простых множителей этих чисел.
- Правило. Чтобы найти НОД нескольких чисел, необходимо:
- — разложить все данные числа на простые множители;
- — отметить одинаковые множители во всех разложениях;
- — найти произведение отмеченных множителей, которое и есть наибольшим общим делителем этих чисел.

НОД (96,36) = 2 *2 *3 = 12.
Следовательно, числа 96 и 36 кратны числам 2, 3, 4, 6, 12. Наибольший делитель из этих чисел — 12, значит,
12 — НОД чисел 96 и 36.
2) Найти НОД чисел 15, 45 и 165.
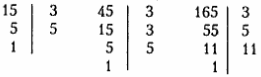
НОД (15, 45. 165) = 3 * 5 = 15.
Следовательно, числа 15, 45 и 165 кратны числам 3, 5 и 15. Наибольший делитель из этих чисел — 15. значит,
15 — НОД чисел 15, 45 и 165.
Для проверки. Наибольший общий делитель (НОД) любого количества чисел всегда меньше или равен наименьшему из них.
Есть числа, которые не имеют другого наибольшего общего делителя, кроме 1.
Например: найти НОД чисел 84 и 715.

НОД (84,715) = 1.
Два числа, наибольший общий делитель которых равен 1, называются взаимно простыми числами.
 SHKOLO.RU
SHKOLO.RU