Пирамида и ее измерения

Пирамида относится к многогранникам (рис. 20).

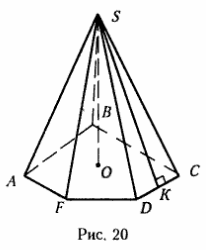
Основанием пирамиды служит многоугольник (ABCDF). Каждая боковая грань пирамиды — это треугольник (ΔASB, ΔBSC, ΔCSD, ΔDSF, ΔASF), ограничивающий ее боковую поверхность и расположенный в своей плоскости. Прямая пересечения каждой пары боковых граней пирамиды — это ее ребра (AS, BS, CS, DS, FS). Все ребра пирамиды пересекаются в одной точке, называемой вершиной пирамиды (S).

Перпендикуляр, опущенный из вершины пирамиды на ее основание, — это высота пирамиды (SO).

Пирамида носит название по многоугольнику, лежащему в ее основании (треугольная, четырехугольная, пятиугольная и т. д.).

На нашем рисунке пятиугольная пирамида, так как в ее основании — пятиугольник. Площадь ее боковой поверхности состоит из площадей пяти треугольников (боковых граней). Каждая грань имеет высоту (SK), которая называется апофемой пирамиды.

Правило. Площадь боковой поверхности пирамиды равна произведению полупериметра основания и апофемы.

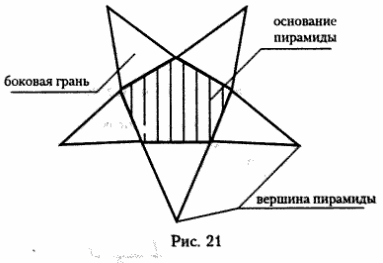
На рис. 21 — развертка пирамиды, приведенной на рис. 20.

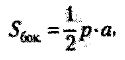
где:
p — периметр основания;
a — апофема.

Правило. Объем пирамиды равен одной трети произведения площади основания и высоты пирамиды.

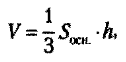
где:
S_осн — площадь многоугольника в основании пирамиды;

h — высота пирамиды.

У пирамид другого вида (наклонных, усеченных) правила нахождения площади и объема другие, иные и формулы для их расчета.