Прямоугольная система координат

Прямоугольная (другие названия — плоская, двухмерная) система координат, названная по имени французского ученого Декарта (1596—1650) «декартовой системой координат на плоскости», образуется пересечением на плоскости под прямым углом (перпендикулярно) двух числовых осей так, что положительная полуось одной направлена вправо (ось x, или ось абсцисс), а второй — вверх (ось y, или ось ординат).

Точка пересечения осей совпадает с точкой 0 каждой из них и называется началом координат.

Для каждой из осей выбирается произвольный масштаб (единичный отрезок длины). Каждой точке плоскости соответствует одна пара чисел, названная координатами этой точки на плоскости. И наоборот, любой упорядоченной паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

Первая координата точки называется абсциссой этой точки, а вторая координата — ординатой.

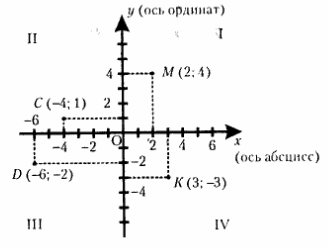
Вся плоскость координат делится на 4 квадранта (четверти). Квадранты расположены от первого до четвертого против часовой стрелки (см. рис.).

Чтобы определить координаты точки, нужно найти ее расстояние до оси абсцисс и оси ординат. Так как расстояние (кратчайшее) определяется по перпендикуляру, то из точки опускаются два перпендикуляра (вспомогательные линии на плоскости координат) на оси так, что точка их пересечения — это и есть место заданной точки в плоскости координат. Точки пересечения перпендикуляров с осями называются проекциями точки на оси координат.

Первый квадрант ограничен положительными полуосями абсцисс и ординат. Следовательно, координаты точек в этой четверти плоскости будут положительными
(знаки « + » и < + »).

Второй квадрант ограничен отрицательной полуосью абсцисс и положительной полуосью ординат. Следовательно, координаты точек по оси абсцисс будут отрицательными (знак «-»), а по оси ординат — положительными (знак « + »).

Третий квадрант ограничен отрицательной полуосью абсцисс и отрицательной полуосью ординат. Следовательно, координаты точек по оси абсцисс и оси ординат будут отрицательными (знаки «-» и «-»).

Четвертый квадрант ограничен положительной полуосью абсцисс и отрицательной полуосью ординат. Следовательно, координаты точек по оси абсцисс будут положительными (знак «+»). а по оси ординат — отрицательными (знак «-»).

Построение точки по ее заданным координатам

1. первую координату точки найдем на оси абсцисс и проведем через нее вспомогательную линию — перпендикуляр;

2. вторую координату точки найдем на оси ординат и проведем через нее вспомогательную линию — перпендикуляр;

3. точка пересечения двух перпендикуляров (вспомогательных линий) и будет соответствовать точке с заданными координатами.