Сокращение дробей
Сократить дробь — значит, используя основное свойство дроби, уменьшить числитель и знаменатель так, что-бы величина дроби при этом не изменилась.
Для сокращения дробей достаточно использовать основное свойство дроби, уменьшая числитель и знаменатель в одинаковое число раз.
Правило. Сократить дробь — значит числитель и знаменатель дроби разделить на одинаковый множитель, отличный от 1, в результате деления дробь записывается числами, величина которых меньше во столько раз, какова величина делителя.
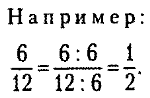
Внимание! Если числитель и знаменатель представлены числовыми или буквенными выражениями, то на слагаемое сокращать нельзя. Сумму (разность), если возможно, надо преобразовать в произведение и сократить на общий множитель числителя и знаменателя дроби.
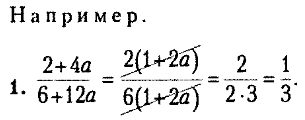
Числитель и знаменатель преобразовали в произведение. Множитель в скобках (1 + 2а) числителя и знаменателя общий, на него можно сократить. Для записи сокращения необходимо одинаковые множители числителя и знаменателя еречеркнуть.
Множители 2 и 6 имеют кратное им число 2, на которое тоже можно сократить дробь.
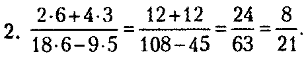
На сумму и разность сокращать нельзя, поэтому в числителе и знаменателе выполнили действия. Полученные сумма и разность имеют общий множитель 3, на который дробь можно сократить.
 SHKOLO.RU
SHKOLO.RU