Разложение составных чисел на простые множители

Составное число всегда можно единственным способом представить как произведение нескольких простых чисел. При арифметических действиях с обыкновенными дробями, если у них разные знаменатели в одном числовом выражении, необходимо привести дроби к сопоставимому виду.

Чтобы произвести такие действия (преобразовать дроби в равновеликие с одинаковыми знаменателями), нужно иметь систему (правило и форму записи) разложения составных чисел на простые множители.

• Правило. Чтобы разложить число на простые множители, надо:
• — записать его слева от вертикальной черты;
• — справа от черты записать первый делитель числа — самое маленькое число из таблицы простых чисел, на которое данное число делится без остатка;
• — в следующей строке слева под числом записать делимое первого этапа, которое является частным от деления данного числа на записанный справа на одной строке с ним делитель;
• — справа найти (как и первый делитель) наименьшее простое число, на которое делимое первого этапа делится без остатка, это число будет вторым делителем числа;
• — слева записать делимое второго этапа, которое есть частное от деления предыдущей строки делимого на ее же делитель;
• — для делимого второго этапа также найти делитель из наименьшего числа простых чисел, записать его на той же строке справа н т. д., пока в делимом последнего этапа не будет стоять 1;
• — делители, стоящие справа от черты, записать множителями данного числа.

Перемножив между собой множители, стоящие справа от черты, мы получаем исходное число.

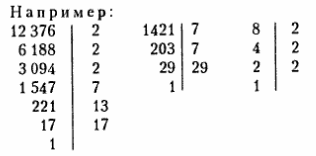
12 376 = 2 * 2 * 2 * 7 * 13 * 17;
1 421 = 7 * 7 * 29;
8 = 2 * 2 * 2.

Внимание! Делители справа у составных чисел увеличиваются слева направо. При разложении на множители простых чисел справа от черты стоит одно число (один делитель) — заданное число, а слева от черты стоят заданное число и число 1.