Отношения

Отношение можно записать как арифметическое действие деление» а можно как обыкновенную дробь. Например, отношения с одинаковым частным: 3:9 и .

Отношением устанавливается взаимная связь однородных величин» предметов, действий. Первоначально же отношение применялось только тогда, когда требовалось выразить одну величину в долях другой величины. Если два отношения имеют один результат вычисления (одинаковое частное), то такие отношения (опуская запись результата) можно соединить знаком равенства.

Например: 3 : 9 = 27 : 81, так как 3 : 9 = и 27 : 81 =

Свойства отношений

Как и в обыкновенной дроби, в отношении можно делимое и делитель (числитель и знаменатель) умножать или делить на одно и то же число, от чего результат не изменится (частное сохраняет свое численное значение).

При вычислении отношения частное может быть:

• 1) больше 1 — значит, отношение характеризует, во сколько раз делимое больше делителя (например, 18:2=*
  9, т.е. делимое больше делителя в 9 раз);

• 2) равно 1 — значит, делимое и делитель — равные величины (например, 5 : 5 = 1, т. е. 5 = 5);

• 3) меньше 1 — значит, частное показывает, какую часть составляет делимое от делителя (например, 3 : 4 = 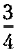= 0,75, т.е. делимое составляет 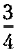от делителя).

Отношение можно выражать в процентах (процентное отношение), для чего частное нужно умножить на 100 и приписать за ним знак процента, что означает, сколько процентов делимое составит от делителя (например, 3:4 = 0,75; 0,75 * 100 = 75%).

Из последнего свойства частного следует: чтобы узнать; сколько процентов составляет одно число от другого, надо взять отношение этих чисел и умножить его на 100, дописав в ответе знак процента.